Student: Jeongbin Jo
Department: Dept. of Physics, College of Science, Yonsei University
Contact: milk_lime@naver.com (jeongbin033@yonsei.ac.kr)
github
https://github.com/dolf3131/QIYA-IBM-Learning
https://github.com/dolf3131/qiskit_algorithms_V2
Introduction
This poster presents the results of the 2025-1 QIYA (Quantum Informatics at Yonsei Academy) IBM Learning Course team project.
- We explored quantum computing topics such as VQA, VQE, VQD, QML, and QSR, based on materials from the IBM Learning Course.
- This poster highlights our implementation of variational quantum algorithms (VQAs) and explores advanced techniques such as Quantum Fisher Information analysis, Quantum Sampling Regression using Gaussian Processes, and surrogate-based optimization.
The full source code and results are available on our GitHub repository.
Variational Quantum Algorithm
- Variational Quantum Algorithm (VQA) is a hybrid approach that combines classical and quantum computing using variational methods.
- The typical workflow of a VQA includes the following steps:
- step 1 Initialize the problem
- step 2 Prepare the ansatz
- $U_R |0\rangle = |\rho\rangle$
- $U_V(\vec{\theta})U_R |0\rangle = U_V(\vec{\theta})|\rho\rangle = |\psi(\theta)\rangle$
- step 3 Evaluate cost function
- $\langle\hat{\mathcal{H}}\rangle_{\psi}:=\sum_{\lambda}\mathfrak{p}_{\lambda}\lambda=\langle\psi|\hat{\mathcal{H}}|\psi\rangle$
- step 4 Optimize the parameters to obtain results
- $\vec{\theta}_{t+1}=\vec{\theta}_{t}-\eta\nabla C(\vec{\theta})$
Quantum Fisher Information
- The Quantum Fisher Information Matrix (QFIM) is the quantum counterpart of the classical Fisher information matrix.
- It quantifies how much information an observable random variable X carries about an unknown parameter in the distribution that models X.
- $\mathcal{F}_{ij}=4~Re[\langle\partial_{i}\psi(\theta)|\partial_{j}\psi(\theta)\rangle - \langle\partial_{i}\psi(\theta)|\psi(\theta)\rangle\langle\psi(\theta)|\partial_{j}\psi(\theta)\rangle]$
- FAdam is an optimizer based on the Fisher information, often referred to as the natural gradient.
- In this project, we investigated a quantum version of FAdam.
- $\vec{\theta}_{t+1}=\vec{\theta}_{t}-\eta F^{-1}\nabla\mathcal{L}(\theta)$
Implementation
We implemented a variational eigensolver using the Quantum Sampling Regression (QSR) framework in combination with a Gaussian process-based surrogate model.
- Ansatz: TwoLocal (ry, entanglement=cz)
- Observable: Arbitrary Hermitian operator
- Sampling: Sobol sequence (quasi-random sampling)
- Surrogate: Gaussian process regression
Quantum Sampling Regression Result
- Quantum Sampling Regression (QSR) is a variational algorithm that approximates a reference function using sampled parameter values.
- As the number of variational parameters increases, the number of required samples grows exponentially. Therefore, QSR is generally not efficient when used with high-dimensional ansätze.
- For sampling, we use Sobol sequences, which are a type of quasi-random low-discrepancy sequence.
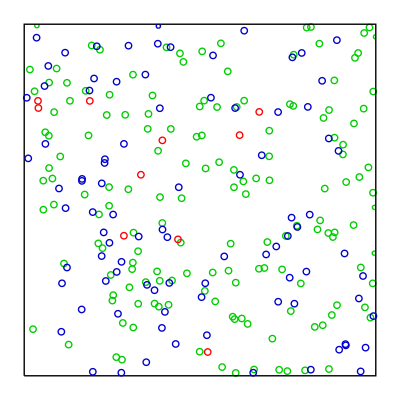 그림 1: Pseudo-random sequence 그림 1: Pseudo-random sequence |
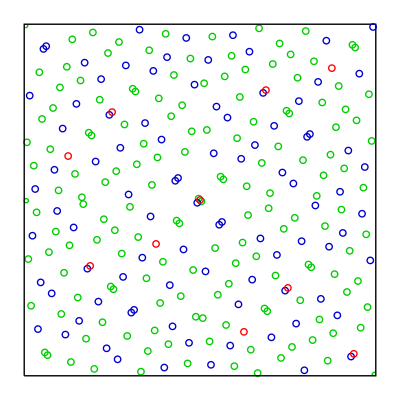 그림 2: Sobol sequence (Quasi-random) 그림 2: Sobol sequence (Quasi-random) |
|---|
Gaussian Process
- A Gaussian Process (GP) is a nonparametric supervised learning method commonly used for regression and probabilistic classification tasks.
- A GP defines a distribution over functions, assuming that any finite set of function values follows a multivariate normal distribution. This makes GPs useful for modeling uncertainty and performing function approximation, especially with limited data.
- (Equation 6) $\mathbb{E}[e^{is^{\top}(X-\mu)}]=e^{-\frac{1}{2}s^{\top}\Sigma s}$
- $X\sim\mathcal{N}(\mu,\Sigma)$ Multivariate normal distribution (vector form)
- $\Sigma$ Covariance matrix
- $\mathfrak{s}\in\mathbb{R}^{n}$ Coefficient vector
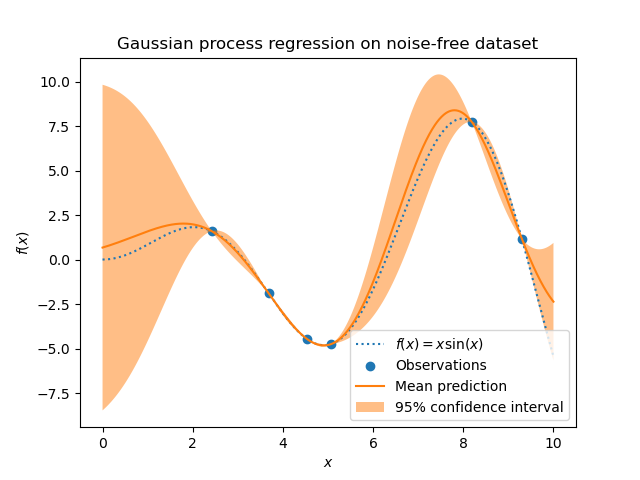
- In terms of computational cost, the surrogate model is significantly cheaper than direct quantum evaluations in the NISQ era.
- Only a single quantum computation of steady-state observables is required, after which the surrogate model can be reused.
- The number of required samples when using Sobol sequences is a power of 2, i.e., $2^{\text{param}}$, where
paramdenotes the number of parameters. However, achieving higher resolution may require even more samples.
Post Project
- QFIM-based sensitivity analysis, natural gradient optimization.
- Diffusion-inspired error-aware learning using inherent NISQ noise.
- Toward noise-leveraged quantum error mitigation.
References
- [1] Gaussian process. URL: https://scikit-learn.org/stable/modules/gaussian_process.html (visited on 06/12/2025).
- [2] Dongseong Hwang. "FAdam: Adam is a Natural Gradient Optimizer using Diagonal Empirical Fisher Information". In: arXiv preprint arXiv:2405.12807v11 (2024). URL: https://arxiv.org/abs/2405.12807v11.
- [3] IBM Quantum Learning: Variational Algorithm Design. URL: https://learning.quantum.ibm.com/ (visited on 06/12/2025).
- [4] Johannes Jakob Meyer. "Fisher Information in Noisy Intermediate-Scale Quantum Applications". In: Quantum (2021). URL: https://quantum-journal.org/papers/q-2021-09-09-539/.
- [5] Pedro Rivero, I. Cloet, and Z. Sullivan. "An optimal quantum sampling regression algorithm for variational eigensolving in the low qubit number regime". In: 2020. DOI: 10.26226/morressier.5fa409874d4e91fe5c54b993.
- [6] Sobol sequence. URL: https://en.wikipedia.org/wiki/Sobol_sequence (visited on 06/12/2025).
'양자컴퓨터' 카테고리의 다른 글
| Computer Science for Quantum Computing (0) | 2025.11.01 |
|---|---|
| 양자 컴퓨팅 구현을 위한 조건: DiVincenzo's Criteria (0) | 2025.11.01 |
| Quantum Mechanics for Quantum Computing (0) | 2025.11.01 |