Qiskit in classroom - Computer science
양자컴퓨팅을 위한 컴퓨터과학 / 도이치-조사 알고리즘편
해당 포스트는 IBM Quantum Platform의 내용을 바탕으로 작성되었습니다.
The Deutsch-Jozsa algorithm
도이치-조사 알고리즘은 특별히 유용한 알고리즘은 아닐 수 있지만, 양자컴퓨터의 효율성, 병렬성 등을 보여줄 수 있다는 점에서 의미가 있다.
양자 컴퓨터의 강점 중 하나는 양자 병렬성(Quantum parallelism)이다. 이는 큐비트의 중첩(superposition)을 이용하여 여러 입력에 대해 동시에 처리할 수 있다는 것이다.
다만 동시에 측정을 할 수는 있어도, 모든 정보를 한 번에 얻어내는 것은 아니다. 이를 알아보기 위해서 도이치-조사 알고리즘을 더 자세히 살펴보자.
Deutsch algorithm
Deutsch 알고리즘은 단일 비트 함수 $f: {0, 1} \to {0, 1}$가 주어졌을 때, 이 함수가 상수 함수(constant function) 인지 (즉, $f(0)=f(1)$) 아니면 균형 함수(balanced function) 인지 (즉, $f(0) \neq f(1)$)를 결정하는 문제이다.
- 상수 함수: $f(0)=0, f(1)=0$ 또는 $f(0)=1, f(1)=1$
- 균형 함수: $f(0)=0, f(1)=1$ 또는 $f(0)=1, f(1)=0$
1. 초기 상태 및 $|\pi_1\rangle$
- 초기 상태: $|1\rangle|0\rangle$
- Hadamard 게이트 적용 후 상태 ( $|\pi_1\rangle$ ):
$$|\pi_1\rangle = |-\rangle|+\rangle = \frac{1}{2}(|0\rangle - |1\rangle)|0\rangle + \frac{1}{2}(|0\rangle - |1\rangle)|1\rangle$$
2. $U_f$ 게이트 적용 후 상태 ($|\pi_2\rangle$)
- $U_f$ 게이트 적용 직후 상태:
$$|\pi_2\rangle = \frac{1}{2} \left( |0\rangle(|0 \oplus f(0)\rangle - |1 \oplus f(0)\rangle) + |1\rangle(|0 \oplus f(1)\rangle - |1 \oplus f(1)\rangle) \right)$$ - 중간 단순화 공식:
$$|0 \oplus a\rangle - |1 \oplus a\rangle = (-1)^a (|0\rangle - |1\rangle)$$
(여기서 $a \in \Sigma$ 즉, $a \in {0, 1}$) - 위 공식을 적용하여 단순화된 $|\pi_2\rangle$:
$$|\pi_2\rangle = \frac{1}{2} \left( (-1)^{f(0)}|0\rangle + (-1)^{f(1)}|1\rangle \right) (|0\rangle - |1\rangle)$$
또는
$$|\pi_2\rangle = |-\rangle \left( \frac{(-1)^{f(0)}|0\rangle + (-1)^{f(1)}|1\rangle}{\sqrt{2}} \right)$$ - 위상 킥백(Phase Kickback)을 반영한 최종 $|\pi_2\rangle$ 표현:
$$|\pi_2\rangle = (-1)^{f(0)}|-\rangle \left( \frac{|0\rangle + (-1)^{f(0) \oplus f(1)}|1\rangle}{\sqrt{2}} \right)$$
이것은 $f(0) \oplus f(1)$ 값에 따라 두 가지 경우로 나뉩니다:- 만약 $f(0) \oplus f(1) = 0$ (함수가 상수인 경우):
$$|\pi_2\rangle = (-1)^{f(0)}|-\rangle|+\rangle$$ - 만약 $f(0) \oplus f(1) = 1$ (함수가 균형인 경우):
$$|\pi_2\rangle = (-1)^{f(0)}|-\rangle|-\rangle$$
- 만약 $f(0) \oplus f(1) = 0$ (함수가 상수인 경우):
3. 최종 Hadamard 게이트 적용 후 상태 ($|\pi_3\rangle$)
- 첫 번째 큐비트에 Hadamard 게이트 적용 후 상태 ($|\pi_3\rangle$):
$$ |\pi_3\rangle = \begin{cases}
(-1)^{f(0)}|-\rangle|0\rangle & \text{if } f(0) \oplus f(1) = 0 \\
(-1)^{f(0)}|-\rangle|1\rangle & \text{if } f(0) \oplus f(1) = 1
\end{cases} $$
고전적 접근 방식의 한계
고전적으로 이 문제를 해결하려면 최소 두 번의 함수 쿼리($f(0)$와 $f(1)$을 각각 계산)가 필요합니다. 두 값을 모두 알아야만 함수가 상수인지 균형인지 판단할 수 있다.
양자적 접근 방식의 우위
Deutsch 알고리즘은 단 한 번의 함수 쿼리 (양자 오라클 호출)만으로 이 문제를 해결할 수 있다. 이는 양자 병렬 처리(Quantum Parallelism) 와 양자 간섭의 원리를 활용하기 때문이다. 하다마르(Hadamard)를 gate를 통해 중첩상태를 만들고 이를 통한 처리를 통해서 양자적 이점을 가져올 수 있다.
실습코드(Deutsch algorithm)
# Load the Qiskit Runtime service
from qiskit_ibm_runtime import QiskitRuntimeService
from qiskit_ibm_runtime import SamplerV2 as Sampler
from qiskit.primitives import BackendSamplerV2
# Load the Aer simulator and generate a noise model based on the currently-selected backend.
from qiskit_aer import AerSimulator
from qiskit_aer.noise import NoiseModel
# Alternatively, load a fake backend with generic properties and define a simulator.
from qiskit.providers.fake_provider import GenericBackendV2
service = QiskitRuntimeService()
backend = service.backend("ibm_yonsei")
print(backend.name)
sampler = Sampler(mode=backend)
noise_model = NoiseModel.from_backend(backend)
# Use AerSimulator for local testing
backend_sim = AerSimulator(noise_model=noise_model)
# backend_sim = AerSimulator.from_backend(backend)
# Use a simulator for testing
sampler_sim = BackendSamplerV2(backend=backend_sim)
# Oracle U_f
from qiskit import QuantumCircuit
def twobit_function(case: int):
"""
Generate a valid two-bit function as a `QuantumCircuit`.
"""
if case not in [1, 2, 3, 4]:
raise ValueError("`case` must be 1, 2, 3, or 4.")
f = QuantumCircuit(2)
if case in [2, 3]:
f.cx(0, 1)
if case in [3, 4]:
f.x(1)
return f## Deutsch's algorithm:
## Step 1: Map the problem
# first, convert oracle circuit (above) to a single gate for drawing purposes. otherwise, the circuit is too large to display
blackbox = twobit_function(
3
).to_gate() # you may edit the number (1-4) inside "twobit_function()" to select among the four valid functions
blackbox.label = "$U_f$"
qc_deutsch = QuantumCircuit(2, 1)
qc_deutsch.x(1)
qc_deutsch.h(range(2))
qc_deutsch.barrier()
qc_deutsch.compose(blackbox, inplace=True)
qc_deutsch.barrier()
qc_deutsch.h(0)
qc_deutsch.measure(0, 0)
qc_deutsch.draw("mpl")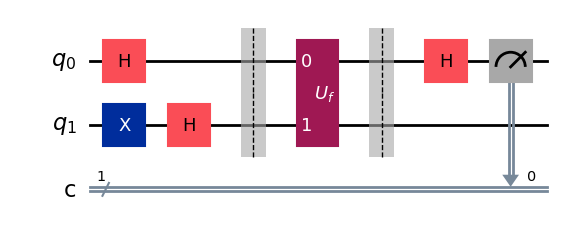
# Step 2: Transpile
from qiskit.transpiler.preset_passmanagers import generate_preset_pass_manager
target = backend_sim.target
pm = generate_preset_pass_manager(target=target, optimization_level=3)
qc_isa = pm.run(qc_deutsch)
# Step 3: Run the job on a real quantum computer
job = sampler_sim.run([qc_isa], shots=1)
# job = sampler_sim.run([qc_isa],shots=1) # uncomment this line to run on simulator instead
res = job.result()
counts = res[0].data.c.get_counts()
# Step 4: Visualize and analyze results
print(counts)
if "1" in counts:
print("balanced")
else:
print("constant")
# Step 5: Visualize and analyze results
from qiskit.visualization import plot_histogram
plot_histogram(counts)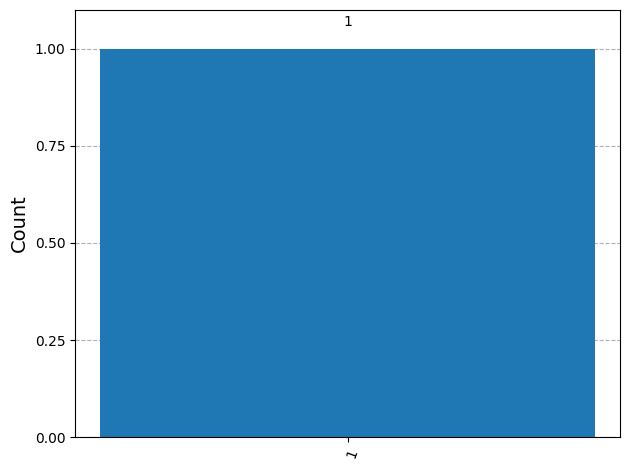
Deutsch-Jozsa algorithm
도이치-조사 알고리즘은 도이치 알고리즘에서 입력을 확장한 것으로, 이렇게 여러 입력에 대해서도 양자 병렬성을 이용하여 한 번의 연산으로 처리할 수 있다는 것이 특징이다. 특히 Bernstein-Vazirani problem 등을 푸는데 활용될 수 있다.
Bernstein-Vazirani problem
Bernstein-Vazirani 문제는 주어진 $n$비트 비밀 문자열 $s$를 알아내는 함수 $f(x) = (s \cdot x) \pmod 2$에 대해 몇 개의 쿼리를 사용하는가 하는 문제이다. 고전적인 경우 n개의 쿼리가 필요하지만 양자컴퓨터를 사용하는 경우 단 하나의 쿼리를 통해 답을 얻을 수 있다.
Bernstein-Vazirani problem
함수 $f: {0,1}^n \to {0,1}$는 $n$비트 입력 $x$를 받아 단일 비트 출력을 반환한다. 이 함수는 알려지지 않은 $n$비트 비밀 문자열 $s$에 대해 항상 $f(x) = s \cdot x \pmod 2$ 관계를 만족한다. 여기서 $s \cdot x$는 비트별 내적(dot product)으로, $s \cdot x = s_{n-1}x_{n-1} \oplus s_{n-2}x_{n-2} \oplus \dots \oplus s_0x_0$ 이다. 우리의 목표는 $s$가 무엇인지 알아내는 것이다.
1. 초기 상태 준비 및 Hadamard 게이트 적용
알고리즘은 $n$개의 입력 큐비트와 1개의 출력 큐비트를 사용한다.
- 입력 큐비트 준비: 모든 $n$개의 입력 큐비트를 $|0\rangle$ 상태로 초기화한다.
- 출력 큐비트 준비: 출력 큐비트를 $|0\rangle$ 상태로 초기화한 뒤, NOT 게이트를 적용하여 $|1\rangle$로 만들고, 이어서 Hadamard 게이트를 적용한다. 이 과정은 출력 큐비트를 $|-\rangle$ 상태로 만든다.
수식으로 표현하면:
초기 상태는 $|0\rangle|0\rangle^{\otimes n}$ 이다.
여기에 해당하는 게이트를 적용한다:
- $$|\Psi_0\rangle = |0\rangle|0\rangle^{\otimes n}$$
1~n번째 입력 큐비트에 $H^{\otimes n}$을, n+1번째 큐비트에 $X$ (NOT) 게이트와 $H$ (Hadamard) 게이트를 적용한다:
$$|\Psi_1\rangle = (HX \otimes H^{\otimes n}) |0\rangle|0\rangle^{\otimes n}$$
각 부분을 계산하면:
- $$H^{\otimes n}|0\rangle^{\otimes n} = \frac{1}{\sqrt{2^n}} \sum_{x \in {0,1}^n} |x\rangle$$
- $$HX|0\rangle = H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle) = |-\rangle$$
따라서, $U_f$ 게이트가 적용되기 전의 상태 $|\Psi\rangle$는 다음과 같다:
- $$|\Psi\rangle = |-\rangle \otimes \left(\frac{1}{\sqrt{2^n}}\sum_{x \in \Sigma^n} |x\rangle\right)$$
2. $U_f$ 게이트 적용
이제 함수 $f$를 구현하는 $U_f$ 게이트를 큐비트들에 적용한다. $U_f$ 게이트는 $|x\rangle|y\rangle$ 상태를 $|x\rangle|y \oplus f(x)\rangle$로 변환한다.
여기서 핵심은 위상 킥백(phase kickback) 메커니즘입니다. 여기에서는 다음을 계산하는 상황이다: $$|- \oplus f(x)\rangle$$
우리는 $|0 \oplus a\rangle - |1 \oplus a\rangle = (-1)^a(|0\rangle - |1\rangle)$ 이라는 것을 알고 있으므로,
- $$U_f |x\rangle |-\rangle = |x\rangle (-1)^{f(x)} \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle) = (-1)^{f(x)} |x\rangle |-\rangle$$
즉, $f(x)$ 값에 해당하는 위상 $(-1)^{f(x)}$이 1~n번째 큐비트 $|x\rangle$에 붙고, n+1번째 큐비트는 여전히 $|-\rangle$ 상태를 유지한다.
따라서 $U_f$ 게이트 적용 후의 상태 $|\Psi\rangle$는 다음과 같다:
- $$|\Psi\rangle = |-\rangle \otimes \frac{1}{\sqrt{2^n}}\sum_{x \in \Sigma^n} (-1)^{f(x)}|x\rangle$$
3. 최종 Hadamard 게이트 적용
이제 처음 $n$개의 입력 큐비트에 다시 Hadamard 게이트의 층($H^{\otimes n}$)을 적용한다. 이는 양자 푸리에 변환과 유사한 역할을 하여 숨겨진 정보를 드러낸다.
Hadamard 게이트는 표준 기저 상태 $|x\rangle$에 적용될 때 다음과 같이 변환된다:
- $$
H^{\otimes n}|x\rangle = \frac{1}{\sqrt{2^n}} \sum_{y \in \Sigma^n} (-1)^{x \cdot y} |y\rangle
$$
이를 활용하여 $|\Psi\rangle = |-\rangle \otimes \left(\frac{1}{\sqrt{2^n}}\sum_{x \in \Sigma^n} (-1)^{f(x)}|x\rangle\right)$ 여기에 $H^{\otimes n}$을 적용하면:
- $$
|\Psi\rangle = |-\rangle \otimes H^{\otimes n} \left( \frac{1}{\sqrt{2^n}}\sum_{x \in \Sigma^n} (-1)^{f(x)}|x\rangle \right)
$$
여기서 $f(x) = s \cdot x$이므로, $H^{\otimes n}$ 안의 항은 $\frac{1}{\sqrt{2^n}}\sum_{x \in \Sigma^n} (-1)^{s \cdot x}|x\rangle$ 가 된다.
이 형태에 $H^{\otimes n}$을 적용하면:
$$
H^{\otimes n} \left( \frac{1}{\sqrt{2^n}}\sum_{x \in \Sigma^n} (-1)^{s \cdot x}|x\rangle \right) \\
= \frac{1}{\sqrt{2^n}}\sum_{x \in \Sigma^n} (-1)^{s \cdot x} \left( \frac{1}{\sqrt{2^n}}\sum_{y \in \Sigma^n} (-1)^{x \cdot y}|y\rangle \right) \\
= \frac{1}{2^n}\sum_{y \in \Sigma^n} \left( \sum_{x \in \Sigma^n} (-1)^{(s \cdot x) \oplus (x \cdot y)} \right) |y\rangle \\
= \frac{1}{2^n}\sum_{y \in \Sigma^n} \left( \sum_{x \in \Sigma^n} (-1)^{(s \oplus y) \cdot x} \right) |y\rangle
$$
여기서 안쪽의 합 $\sum_{x \in \Sigma^n} (-1)^{(s \oplus y) \cdot x}$ 은 Kronecker delta ($\delta$)와 유사하게 작동한다:
- 만약 $s \oplus y = \mathbf{0}$ (즉, $s=y$) 이면, 모든 $x$에 대해 $(s \oplus y) \cdot x = 0$ 이므로, 합은 $\sum_{x \in \Sigma^n} (-1)^0 = \sum_{x \in \Sigma^n} 1 = 2^n$ 이 된다.
- 만약 $s \oplus y \neq \mathbf{0}$ 이면, 합은 정확히 $0$이 된다. (균형 함수에 Hadamard를 적용했을 때 0이 되는 원리)
따라서 전체 식은 $y=s$인 항만 남게 되어:
- $$= \frac{1}{2^n} \left( 2^n |s\rangle \right) = |s\rangle$$
결론적으로, 최종 Hadamard 게이트 적용 후의 상태는 다음과 같다:
- $$|\Psi\rangle = |-\rangle \otimes |s\rangle$$
4. 측정 및 비밀 문자열 추출
마지막 단계는 처음 $n$개의 큐비트를 측정하는 것이다.
위에서 도출된 최종 상태 $|\Psi\rangle = |-\rangle \otimes |s\rangle$ 에서, 입력 큐비트들은 정확히 비밀 문자열 $s$를 나타내는 상태에 있다.
따라서 처음 $n$개의 큐비트를 측정하면, 우리는 100% 확률로 비밀 문자열 $s$를 얻게된다.
이 과정은 단 한 번의 양자 오라클 $U_f$ 쿼리만으로 $n$비트의 비밀 문자열 $s$를 알아낼 수 있음을 보여준다. 고전적인 방법으로는 $n$번의 쿼리가 필요했던 것과 비교하면 양자 컴퓨터의 압도적인 속도 향상을 명확히 보여주고 있다.
실습코드(Deutsch-Jozsa, Bernstein-Vazirani problem)
# Step 1: Map the problem
def bv_function(s):
"""
Create a Bernstein-Vazirani function from a string of 1s and 0s.
"""
qc = QuantumCircuit(len(s) + 1)
for index, bit in enumerate(reversed(s)):
if bit == "1":
qc.cx(index, len(s))
return qc
display(bv_function("1000").draw("mpl"))string = "1000" # secret string that we'll pretend we don't know or have access to
n = len(string)
qc = QuantumCircuit(n + 1, n)
qc.x(n)
qc.h(range(n + 1))
qc.barrier()
# qc.compose(oracle, inplace = True)
qc.compose(bv_function(string), inplace=True)
qc.barrier()
qc.h(range(n))
qc.measure(range(n), range(n))
qc.draw("mpl")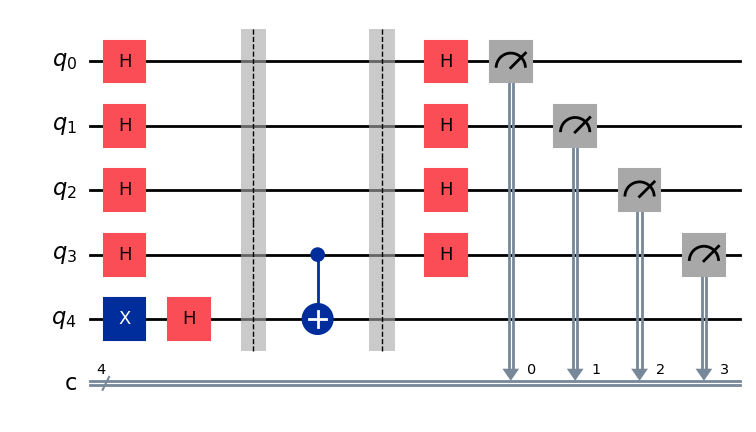
# Step 2: Transpile
from qiskit.transpiler.preset_passmanagers import generate_preset_pass_manager
target = backend.target
pm = generate_preset_pass_manager(target=target, optimization_level=3)
qc_isa = pm.run(qc)
# Step 3: Run the job on a real quantum computer
job = sampler_sim.run([qc_isa], shots=1)
# job = sampler_sim.run([qc_isa],shots=1) # uncomment this line to run on simulator instead
res = job.result()
counts = res[0].data.c.get_counts()
# job = sampler_gen.run([qc_isa],shots=1)
# res=job.result()
# counts=res[0].data.c.get_counts()
# Step 4: Visualize and analyze results
## Analysis
print(counts)
# Step 5: Visualize and analyze results
from qiskit.visualization import plot_histogram
plot_histogram(counts, title="Bernstein-Vazirani counts") 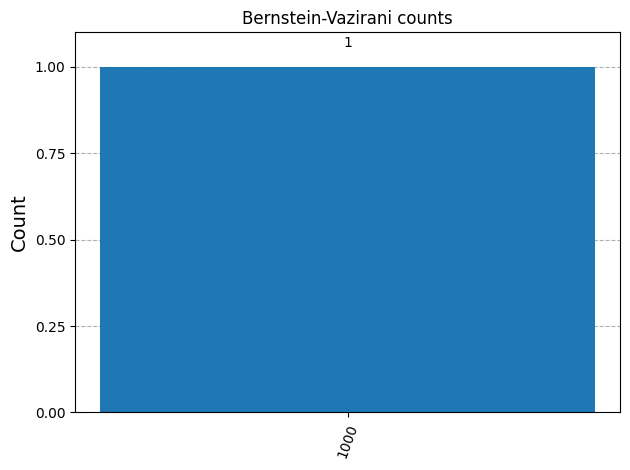
결론
Deutsch-Jozsa 알고리즘은 양자 컴퓨팅의 초기 발전 단계에서 양자 우위의 가능성을 입증하였다. 비록 직접적인 상업적 응용은 제한적일지라도, 이는 양자 알고리즘 설계의 기본 원리를 확립하고 미래 양자 기술의 발전을 위한 필수적인 토대를 마련했다고 볼 수 있다.
참고문헌
Qiskit in the classroom - computer science
IBM Quantum Learning - Fundamentals of quantum algorithms
'양자컴퓨터' 카테고리의 다른 글
| 양자 컴퓨팅 구현을 위한 조건: DiVincenzo's Criteria (0) | 2025.11.01 |
|---|---|
| Quantum Mechanics for Quantum Computing (0) | 2025.11.01 |
| 2025-1 QIYA (Quantum Informatics at Yonsei Academy) IBM Learning Course Team Project (0) | 2025.10.31 |